Mathematics With Dr. Vince

Quick links

Updates
Schedule
Homework
Exams
Online resources
Practice problems
Challenges
Logistics

Updates

MasterChef Calculus auction lot order

Schedule

Tentative schedule for upcoming classes:

Week of Jun. 9
- Monday, Jun. 9: Newton’s Law of Cooling and forensics (2514/2515)
- Wednesday, Jun. 11: Spare (Unit 10 re-write in 2307)
- Friday, Jun. 13: Spare
Week of Jun. 16
- Monday, Jun. 16: MasterChef Calculus (2307)
- Wednesday, Jun. 18: Spare
- Friday, Jun. 20: Spare
Week of Jun. 23
- Monday, Jun. 23: Last class activities (2307)
- Wednesday, Jun. 25: No class (half-day)

Homework

If you are consistently spending more than 1 hour per day on homework, please see me. (Nearly) Every section we cover will have an associated AP Classroom online homework for you to complete by a certain deadline, typically before the next class (or in the case of a test, the class after that). You will also receive paper assignments from Flipped Math to work on. Any additional homework outside of these two will be posted here.

Homework for Friday, December 13:

10.1 Q1-37 (odd only, skip 17)

Homework for Monday, September 9:

Introduction Questionnaire

Exams

Unit 10 final unit test scheduled for Monday, March 24 in-class. You should be proficient in all material contained in Unit 10, though the majority of questions will focus on 10.10-10.15. More precisely, you should be able to:

Determine convergence or divergence of a series using:
- its partial sums
- geometric series (and know the value of the sum if it converges)
- nth term test
- p-series
- comparison tests
- alternating series test
- ratio test
- absolute convergence
Apply the AST error bound
Find and use the Taylor or Maclaurin polynomial of a function
Apply the Lagrange error bound
Find the radius and interval of convergence of a power series
Find Taylor and Maclaurin series of a function
- this includes using known series to generate new series via substitution, addition/subtraction/multiplication/division, differentiation, or integration

Exam weighting: 17.5

NOTE: any material from Units 1 to 9 as well as 10.1-10.9 is also fair game and may be useful/necessary.

Final exam information: 8:00AM, Monday, May 12, 5th floor 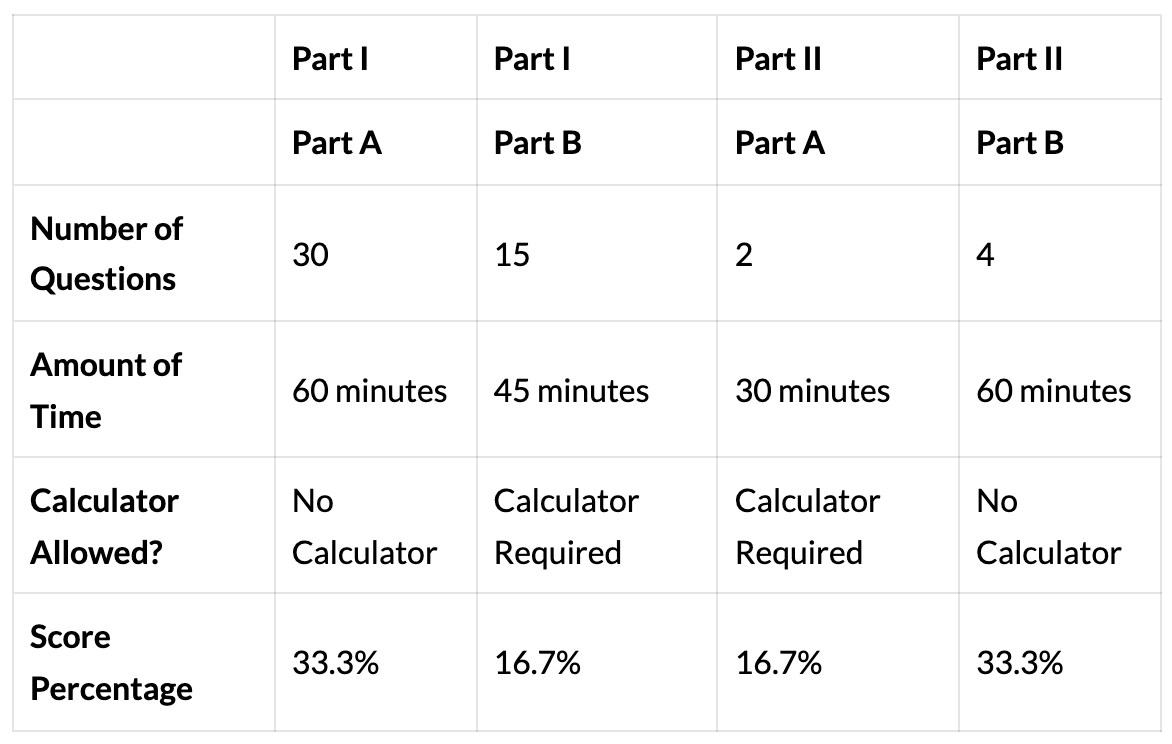Part I tests are MCQ and Part II tests are FRQ

Online resources

The Essence of Calculus YouTube series (brought to you by 3 Blue 1 Brown)
AP Calculus BC course (Khan Academy)
Online calculator (WolframAlpha)
Online graphing program (Desmos)
Brachistochrone curve
- Short by ActionLab
- 16 minute in-depth video by 3Blue1Brown
Interactive visualization of the Chain Rule
Optimization problems
- Visualization of: Cable to two points
- Visualization of: Distance from point to square root graph
Concavity
- Visualization of the relationship between a curve’s concavity, its tangent line, and the second derivative
Trigonometry
- The etymology of the 6 standard trig functions, complete with animations
- Proofs of Trigonometric Derivatives
DE
- Slope field plotter
- Derivation of logistic model formulae
Integration

Practice problems

Calculus readiness test (Answers)
Unit 1
- Limits (graphical) (Answers)
Unit 3-5
- Derivative practice (not comprehensive, answers included)
Unit 6
Unit 7
- Slope Fields practice 1 (Solutions)
- Slope Fields practice 2 (Solutions)
Unit 8
- Practice with volumes 1 (specific examples) (Solutions)
- Practice with volumes 2 (more general examples) (Solutions)
Unit 10
- Some practice testing series (10.1-10.9) (Answers)

Mini-maths

Challenges

Calculus-based:

Unit 1: A weird limit - Find an example of a function whose limit at 0 from the right DNE.
Unit 1: Continuous nowhere - Does there exist a function which is continuous nowhere?
Unit 1: Continuous on the irrationals - Does there exist a function which is continuous only on the irrationals?
Unit 1: Continuous on the rationals - Does there exist a function which is continuous only on the rationals?
Unit 2: Continuous but not differentiable - Does there exist a function which is continuous everywhere but not differentiable infinitely often?
Unit 2: Differentiability for piecewise - Prove you can use derivatives from the left and right to determine differentiability for piecewise functions.
Unit 3: Continuous but nowhere differentiable - Does there exist a function which is continuous everywhere but differentiable nowhere?
Unit 6: An integral - Evaluate this integral.
Unit 6: Integration by parts - Evaluate this integral using integration by parts.
Unit 6: Coefficients in a partial fraction decomposition - Why are we allowed to use values of x for which the original expression is undefined?
Unit 6: An improper integral - Evaluate this improper integral.
Unit 7: division by 0 in separation of variables - Find an example where you have to be more careful about separation of variables
Unit 9: bat curve - Find a function whose graph matches mine
Unit 10: A Challenging Series - Find the exact value of this non-geometric series
Unit 10: Sparse Harmonic Series - Show that if we remove certain terms from the harmonic series, we get convergence
Unit 10: Divergence Test II - Prove that even if n times the summands do not converge to 0, then the series divereges
Unit 10: Sum of Product - Prove that the product of summands from convergent series is convergent

Assorted: